목차
Subspace
우리는 지난 시간에 Vector space 에 대해 배웠다.
어떤 \( \{ V,+,\cdot\}\) 가 K위의 벡터공간이라고 하는 것은, V 속의 임의의 벡터와 K의 임의의 상수에 대해, 10가지조건 (덧셈에 대해 닫혀있다, 상수곱에 대해 닫혀있다. 덧셈의 역원, 항등원이 존재한다. 곱셈의 항등원이 존재한다 등)을 만족시킨다는 뜻이라고 배웠다.
이번 시간에는 V의 부분집합(W)에 대해, 그것이 V로부터 같은 연산을 물려받아 정의된 \( \{ W,+,\cdot\}\)가 이 역시 K위에 정의된 Vector space인 경우에 대해 배울 것이다. 알아두어야 할 점은, \( \{ V,+,\cdot\}\)가 벡터공간이라고 V의 부분집합도 반드시 벡터공간인것은 아니라는 것이다.
definition
\( \{ V,+,\cdot\}\) 가 K-vector space일때, V의 부분집합(subset) W에 대하여, \( \{ W,+,\cdot\}\) 또한 K-vector space 이면, W를 a subspace of V라고 부른다.
examples of subspaces and non-subspaces
세 가지 예시를 살펴보고 이것들이 subspace인지 아닌지 판별해보자. 아래의 경우에서 덧셈과 상수곱은 잘 알려진 일반적인 연산이라 가정한다.
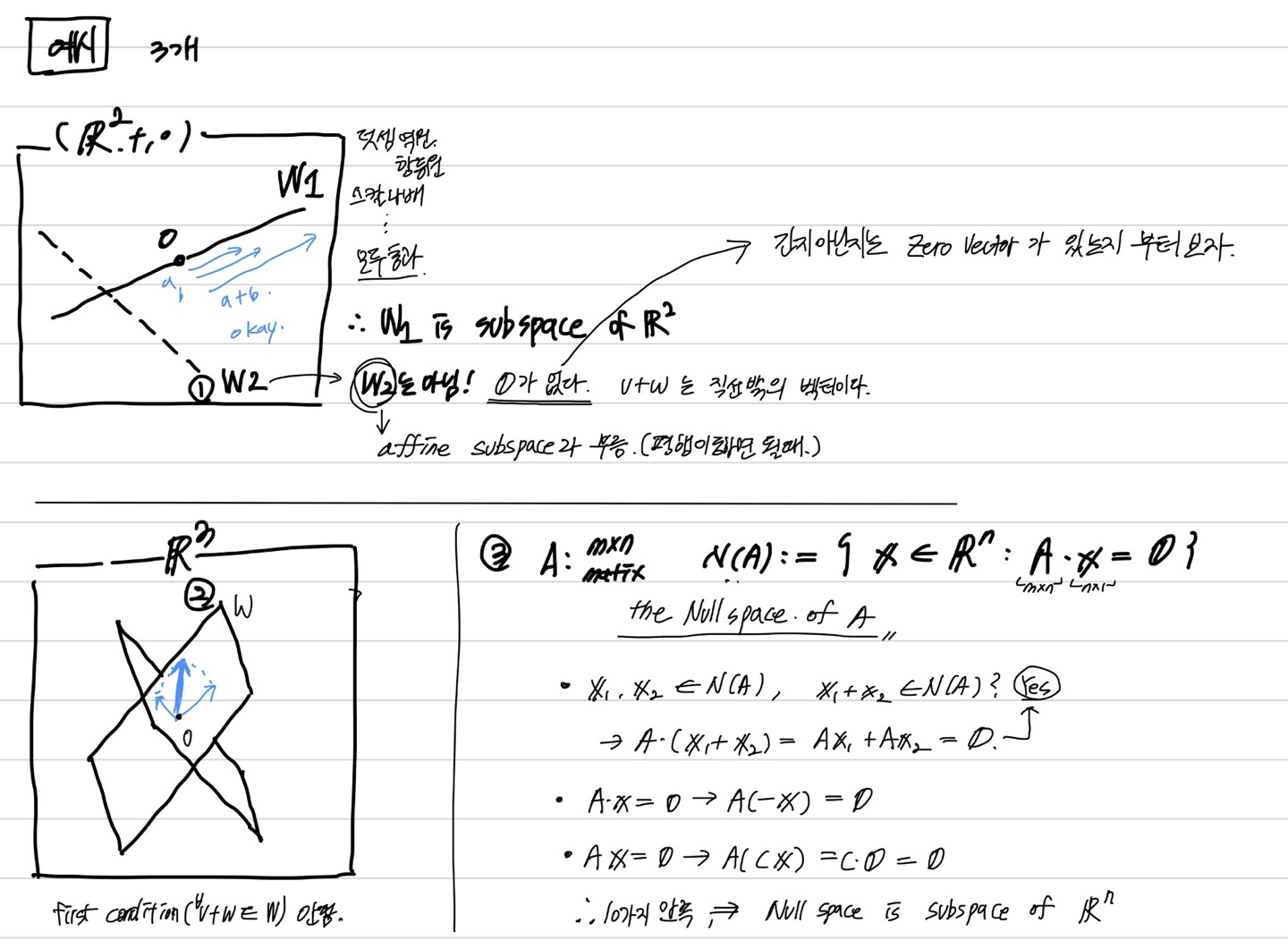
R^2 공간 안에 정의된 원점을 지나는 직선
subspace이다. "원점을 지나기 때문에" 두벡터를 더한 벡터도 직선위의 점이고, 어떤 벡터에 상수배 한것도 직선위의 점이다. 이외에도 영벡터가 덧셈에 대한 항등원이고, 원점 대칭 벡터가 덧셈에 대한 역원이다.
그러나, 만약 "원점을 지나지 않는 직선"이라면, 이것은 subspace가 아니다. 그러나 이 경우 이 녀석을 평행이동만 시켜도 subspace가 되므로, 이런 경우를 affine subspace 라고 부른다.
R^3 공간에 정의된 두 평면의 집합
subspace가 아니다. 이 경우는, 두벡터에 대해 덧셈이 닫혀있지 않기 때문이다. 각각의 평면에서 한 벡터씩 잡으면, 두 평면에 모두 속하지 않은 새로운 벡터가 된다.
Nullspace of A
Nullspace N(A) 는 다음과 같이 정의한다. \[ N(A) = \left \{ x \in \mathbb{R}^n : A \cdot x = 0 \right \}\]
어떤 행렬 A를 하나의 계수행렬이라 정의하고 그것이 0이 되게 하는 근의 집합을 null space라고 한다. 이때 이것은 subspace이다. 임의의 두근에 대해 이들을 합하거나 상수배 한 값 역시 근이 되기 때문이다. -1배 한 근은 덧셈 역원이 되고, 0배 한 근은 덧셈의 항등원이 된다.
linear combination of vectors
Subspace인지 아닌지는 선형결합에 대해 닫혀있느냐(closed to sum and scala multiplication).
위에서 보면서 눈치 챘을수도 있지만, 벡터공간의 부분집합이 subspace인지 아닌지를 판별할 때 중요한 것은 어떤 벡터들의 합과 상수곱에 의해서 닫혀있는지의 여부이다. 이전에 벡터공간 판별 10가지 조건을 이야기 했지만, 어떤 벡터공간의 부분집합이 Subspace인지를 판별할땐 그것들은 전부 2가지 성질로 환원(reduction)된다. 그 두가지가 방금 말한 "덧셈에 대한 닫힘(closure)" 과 "상수곱에 대한 닫힘(closure)" 이다. 벡터 공간의 항등원 0 벡터 존재성은 벡터 덧셈 v + (-v) 의 닫힘으로 환원되고, 덧셈의 역원 -v 벡터의 존재성은 상수곱 (-1) * v 의 닫힘으로 환원된다.벡터공간에 속한 임의의 벡터를 추출하여, 각각의 연산을 적용해 출력된 새로운 벡터역시 그 벡터공간의 원소임을 의미한다. 그리고 이 두 조건은 다시 하나로 합쳐져 "linear combination"이라는 하나의 표현으로 압축된다.
linear combination
그래서 두 벡터의 합과 상수곱을 하나로 합쳐, 우리가 \( c_1v_1+c_2v_2\) 로 나타낼 수 있고, 이를 두 벡터의 linear combination(선형결합)이라 부른다. 이를 n개 벡터로 확장하면, \[ \lambda _1 v_1+\lambda _2 v_2+\lambda _3 v_3 + ... + \lambda _k v_k\] 로 나타낼 수 있고, 이것을 k개의 벡터 \(v_1, v_2, ..., v_k\)의 linear combination이라 부른다.
우리가 linear combination을 통해 얻을 수 있는 편리함은, 임의의 벡터공간의 모든 벡터를 linear combination으로 나타낼 수 있다는 점이다. 예를 들어 두 벡터 v와 w 가 이루는 선분, 직선, 평면은 두벡터의 선형결합과 계수들의 구속조건으로 나타낼 수있다. (아래 그림)

그렇다면 우리는 어떤 집합 \( \{ V,+,\cdot\}\) 가 K-vector space이라는 조건을 아래 한문장으로 축약시켜 적을 수 있다.
\( \{ V,+,\cdot\}\) 가 K-vector space 이라면, V의 임의의 k개의 벡터 \(v_1, v_2, ..., v_k\) 에 대하여, 그것들의 선형결합\( \lambda _1 v_1+\lambda _2 v_2+\lambda _3 v_3 + ... + \lambda _k v_k\) 도 V의 원소이다.
\[ \{ V,+,\cdot\} \: is \: K-vector\: space\: \Leftrightarrow\:\lambda _1 v_1+\lambda _2 v_2+\lambda _3 v_3 + ... + \lambda _k v_k \in V \]
v1, ..., vk가 만드는 subspace
이제 우리는 반대로, 임의의 k개의 벡터가 선형결합을 이루어 만드는 vector space에 대해 살펴보려고 한다. 임의의 k개의 벡터가 만드는 모든 선형결합 벡터들의 집합을 span 이라 하고,
\[span\{v_1, v_2, ..., v_k\} = \{all\: possible\: linear\: combination\: of\: v_1, v_2, ..., v_k\}\]
\[<v_1, v_2, ..., v_k> = \{\lambda _1 v_1+\lambda _2 v_2+\lambda _3 v_3 + ... + \lambda _k v_k \}\]
로 나타낸다.
그런데 여기서 하나의 벡터를 여러 벡터의 선형결합으로 나타낼 수 있는데, 과연 그 조합이 유일할까?
A 벡터를 나머지 k-1개의 벡터로 나타낼때, 이렇게 조합해도 되고 저렇게 조합해도 되지 않을까? (그러면 다루기 까다로워진다) 그렇다면, 유일하게 나타내기 위해선 어떤 조건이 필요할까?
Linear independance
선형 독립이란, 어떤 k개의 벡터의 선형결합이 0벡터가 될 때, 모든 계수가 0인 경우(trivial case) 말고는 더 이상의 경우가 존재하지 않을때(다른 말로 trivial case가 유일한 해일 때) \(v_1, v_2, ..., v_k\) 는 linearly independant 하다고한다. linearly dependant 하다는 것은 다른말로는 어느 벡터 하나가 다른 벡터들의 선형결합으로 표현 가능하다는 것을 의미한다. 다시말해 그 벡터는 불필요한(redundant) 벡터라는 것이다.

그 증명은 아주쉽게 가능하다. 만약 계수가 0이 아닌 것이 존재한다면, 그녀석을 제외한 나머지 성분을 우변으로 이항시키고, 0이 아닌 계수로 나눗셈을 한다면 결국 그 벡터는 나머지 벡터들의 선형결합이 된다.
basis
여기서 새로운 개념이 등장하는데, 어떤 벡터공간 V의 벡터의 집합 S = \( \{ v_1, v_2, ..., v_k \} \) 에 대하여, 만약 아래 두조건을 만족한다면
- \(<v_1, v_2, ..., v_k> = V\) : k개의 벡터의 선형결합이 벡터공간 V의 모든 벡터를 span 한다.
- S = \( \{ v_1, v_2, ..., v_k \} \)가 linearly independant 하다.
이때 S = \( \{ v_1, v_2, ..., v_k \} \)를 벡터공간 V의 basis(기저)라 부른다.
'Math > 선형대수학 Linear Algebra' 카테고리의 다른 글
| [4-1] Crammer's Rule, Adjoint, Vector Space (0) | 2023.03.20 |
|---|---|
| 3-2 Determinant (0) | 2023.03.16 |
| [3-1] Inverse Matrix (0) | 2023.03.13 |
| [2-1 , 2-2] Matrix (0) | 2023.03.12 |
| [1-1,1-2] Introduction to Linear Algebra (0) | 2023.03.06 |




댓글