목차
Matrix Basics
행렬 A를 간단하게 i번째 행, j번째 열의 원소의 집합이라는 의미에서 다음과 같이 나타내기도 한다. $A = \left ( a_{ij} \right )$
정의되는 연산들
- 덧셈 Addition : 사이즈가 같은 행렬만 가능 $ A + B = \sum (a_{ij} + b_{ij})_{m \times n}$
- 상수 곱 Scalar multiplication : $kA = \sum ka_{ij}$
- 행렬 곱 Matrix multiplication : 앞 행렬의 열 수와 뒤 행렬의 행 수가 같아야 곱이 정의된다.
$$AB_{ij} = a_{i1}+b_{1j}+a_{i2}+b_{2j}+ ... + a_{ip}+b_{pj}=\sum_{k = 1}^{p}(a_{ik} b_{kj}) $$
Generalization
우리는 하나의 벡터도 nx1 행렬로 볼 수있다. 심지어 스칼라도 1x1 행렬로 볼 수 있다. 이를 따르면 우리는 하나의 방정식을 행렬곱으로 나타낼 수 있다.
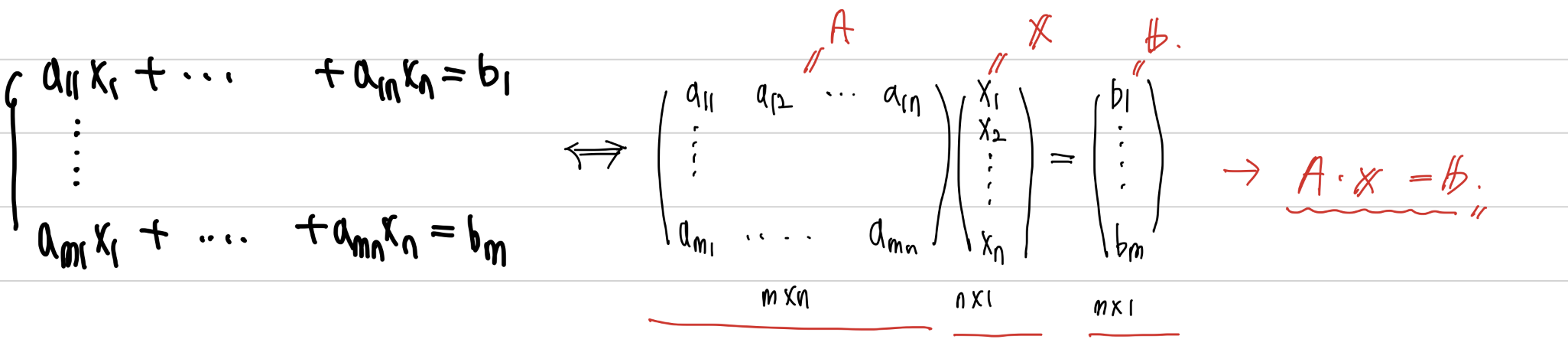
행렬곱을 이해하는 3가지 방법

- 첫번째, 가로행 벡터들의 집합이라고 본다. 왼쪽 가로벡터의 각 성분이 쪼개져 오른쪽 각 가로벡터에 곱해진 뒤 합쳐진다. 이 합쳐진 것이 다시 하나의 가로벡터를 형성한다.
- 두번째, 세로행 벡터들의 집합으로 본다. 우측 세로벡터의 각 성분이 쪼개져 왼쪽 세로벡터에 곱해진 뒤 합쳐진다. 이 합쳐진 것이 다시 하나의 세로벡터를 형성한다.
- 세번째, 세로행 벡터와 가로행 벡터의 곱으로 생각한다. 이 각각의 세로행 벡터-가로행 벡터 곱은 원래 행렬곱으로 나오는 행렬과 같은 사이즈의 행렬을 뱉어낸다. 각각의 한쌍 곱이 만든 새로운 행렬들을 전부 더한게 전체 행렬의 곱이라고 이해한다.
Properites
- 일반적으로 교환법칙은 성립하지 않는다. 단 둘이 정방행렬이고 하나가 Elementary 행렬일때는 가능하다. $AB \neq BA$ but $A_{n \times n}I_n = I_nA_{n \times n}$
- 결합법칙 성립 A(BC) = (AB)C
- k(AB) = A(kB)
- $B=C \to AB = AC$ 역은 성립하지 않는다.
- $A^{p+q} = A^p \times A^q$
Transpose (전치)
A의 행과 열을 뒤집는 행위를 의미한다. $$A = \sum a_{ij} , \: A^T = \sum a_{ji}$$
- $(A^T)^T = A$
- $(A+B)^T = A^T + B^T$
- 증명 : $A_{ij}^{T} + B_{ij}^{T} = A_{ji} + B_{ji} = (A+B)_{ji} = (A+B)_{ij}^{T}$
- $(AB)^T = B^T A^T$
- 증명 : $(B^T A^T)_{ij} = \sum(B_{ik}^T A_{kj}^T) = \sum(B_{ki} A_{jk})= \sum(A_{jk}B_{ki}) = AB_{ji} = (AB)_{ij}^T$
Symmetry and Skew Symmetry

- Symmetry : $A = A^T$ : 대각성분은 뭐든 상관없고, 양쪽 삼각형이 대칭
- Skew Symmetry $A = -A^T$ : 대각성분이 0이고 양쪽 삼각형이 부호가 반대이면서 대칭
Fact : 모든 행렬은 symmetry + skew-symmetry 꼴로 나타낼 수 있다! $$ M = \frac{(M+M^T)}{2} + \frac{(M-M^T)}{2} $$
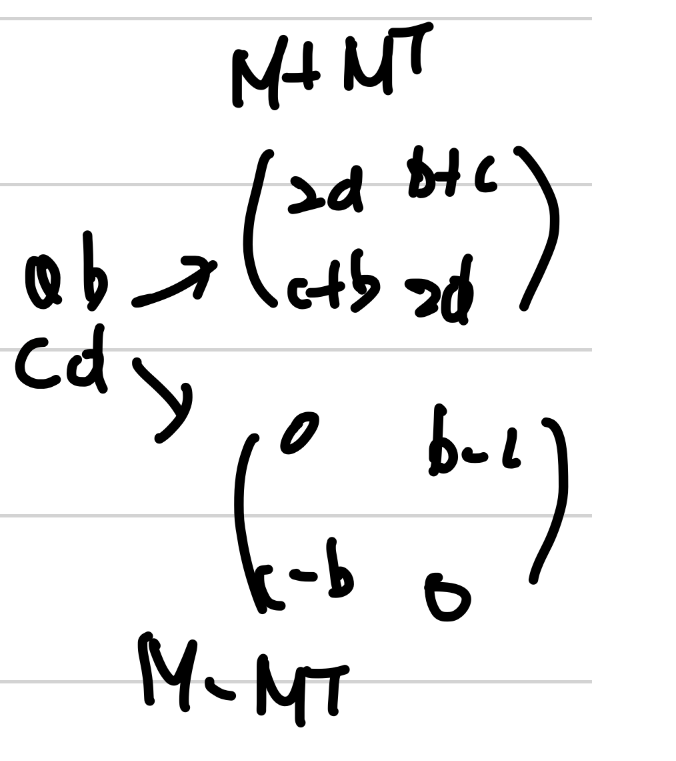
Block을 나누어 행렬곱하기

행렬을 블록단위로 나누어, 각각의 블록이 하나의 Element인 것 처럼 계산한다. (이건 컴퓨터가 크기가 큰 행렬을 recurssive하게 계산하는 원리가 된다. ) 위 그림과 같이 행렬곱을 블록을 나누어 할 수 있는데, 여기서 중요한 건 행렬의 사이즈를 잘 고려해서 블록을 구분해야한다는 것이다. 예를 들어 뒤에 행렬을 2x2 행렬과 3x2행렬로 나누었으면, 앞의 행렬은 col의 수가 2와 3이 되도록 줄을 갈라야 한다. 즉 세로줄을 2열과 3열 사이에 둬야 한다. 그렇다면 앞의 행렬의 가로줄은 무엇을 고려해서 그으면 될까? 그건 상관없다. 어차피 앞 행렬의 열 수와 뒤 행렬의 행 수만 맞으면 되기 때문이다.
'Math > 선형대수학 Linear Algebra' 카테고리의 다른 글
| [4-2] Subspace, Linear combination, linearly independant (0) | 2023.03.23 |
|---|---|
| [4-1] Crammer's Rule, Adjoint, Vector Space (0) | 2023.03.20 |
| 3-2 Determinant (0) | 2023.03.16 |
| [3-1] Inverse Matrix (0) | 2023.03.13 |
| [1-1,1-2] Introduction to Linear Algebra (0) | 2023.03.06 |




댓글