목차
Determinant (행렬식)
개요 (Introduction)
Determinant is a Set function
Determinant 는 Set function이다. nxn 행렬이 모여있는 집합의 원소인 하나의 행렬에 실수(가 아니고 Complex number일수도 있음) 하나를 대응시키는 (real number일 경우) Real valued function이다.
Determinant의 기하적 의미 (2, 3 dimensional view)
행렬식의 절댓값은, 2차원에선 두 벡터가 이루는 평행사변형이 되고, 3차원에서는 세 벡터가 이루는 평행육면체의 부피(triple product)가 된다. 그렇기 때문에 행렬식이 0이라는 것은 2차원에서는 두 벡터가 평행하여 평행사변형의 넓이가 0이 되는 것이고, 3차원에서는 어느 한벡터가 다른 두 벡터가 이루는 평면 위의 벡터라서 평행 육면체의 부피가 0이 되는 것이다.
Determinant can be used for ~
그래서 행렬식은 0이냐 0이 아니냐는 2가지를 결정한다. 첫번째로 Linear independency를 결정한다. Determinat가 0이면 행렬의 각 열벡터들이 linearly dependant하다고 하고, 0이 아니면 linearly independant 하다고 한다. 즉 행렬식은 어느 한 행렬의 독립성을 판단하는 함수로 쓰일 수 있다.
또한 A matrix가 Inversible 한지를 결정한다. Det가 0이 아닐때만 그 행렬은 Inversible하다고 말할 수 있다. (이는 후에 설명하겠다.)
What is the probability that a randomly selected matrix's determinant is equal to zero?
그렇다면 우리가 임의의 행렬을 골라서 행렬식을 계산했을 때, 그것이 0이 될 확률은 무엇일까? 임의의 NxN matrix에서, 임의로 고른 행렬의 Determinant가 0이 될 확률은 0%이다. 그 이유는 다음과 같다,

우리가 n by n 행렬의 행렬식을 구할 때, 그건 최고차항의 차수(degree)가 n이고, 항의 개수가 n^2개인 다항식(polynomial)이다. 만약 n by n matrix의 집합을 위 그림처럼 공간에 점을 찍어 놓고, 그 중에 Det가 0이 되는 점들만을 고른다는 것은, 공간에 구속 조건 하나를 더하는 것과 같다. 예를들어 3차원 공간에서 구속 조건을 하나 만족시키는 점들의 집합은 곡면이다. 이 곡면에 대응되는 확률은 0이다. Probability density function의 degree가 낮은 집합에 대응되는 확률은 0이기 때문이다. 그렇다고 determinant가 0인 행렬이 없다는 말은 아니고, 그 양의 비율을 따졌을때 determinant가 0이 되지 않는 행렬의 개수의 비율이 무수히 크기 때문에 "확률상" 0이라고 말하는 것이다.
따라서, 우리가 임의의 행렬을 선택했을때 그 행렬이 충분히 클 경우, 우리는 100%의 확률로 그 행렬이 linearly independant하고 Inversible 하다고 생각할 수 있다. (Det = 0)
Definition of Determinant with Cycle Notation
Definition
Cycle notation을 활영하여 아래와 같이 정의한다.
\[det(A) = \sum_{\sigma \in S_n}sign(\sigma) \cdot a_{\sigma(1)1}\cdot a_{\sigma(2)2}\cdot...\cdot a_{\sigma(n)n} \]
위의 경우에서 각각의 알쏭달쏭한 sigma와 S 그리고 sign에 대해 설명하겠다.
Cycle notation
우선 \( S_n\)은 무엇을 의미하냐면, 어떤 n개의 원소가 있을때 가능한 Permutation의 집합이다. 예를 들어 n = 3이면 \[ S_n = {(1,2,3),(1,3,2) ,(2,1,3), (2,3,1), (3,1,2), (3,2,1)}\] 이다.
\(\sigma\) 는 이 \( S_n\)의 하나 하나의 원소를 의미한다. 그렇다면 \( a_{\sigma(1)1} \) 은 무엇이냐, 예를 들어, \(\sigma\)가 (3,1,2) 이라 하자, 그러면 \[\sigma(1) = 3, \sigma(2) = 1, \sigma(3) = 2 \] 이다. 따라서 \[a_{\sigma(1)1} = a_{31}\] 을 의미한다.
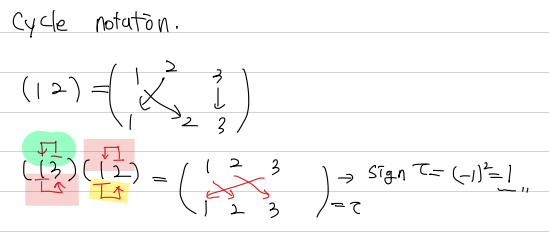
그리고 우리는 하나더 배워야 할 것이 있는데, 각각의 Permutation은 길이가 2인 변환의 합성 함수로서 나타낼 수 있다는 것이다. 예를 들어 (3,1,2)는 (1,3)(2,3) 로 나타낼 수 있다. 오른쪽 부터 읽는 것이다. 예를 들어 3의 경우, 3에서 2로 가고 2에 대해서는 더 적혀 있는게 없으므로 2가 된다. 그래서 세번째 자리가 2이다. 2의 경우, 2에서 3으로 가고, 다시 3에서 1로 가므로 두번째 자리는 1이다. 마지막으로 1의 경우 1에서 3으로 가므로 3이다. 임의의 Permutation은 이 합성함수 방식으로 나타낼 수 있고, 이를 Cycle notation 이라 부른다.
what is sign of \( \sigma \)
Sign 이라 함은, 어떤 Permuation이 몇개의 합성함수로 나타냈느냐에 따라, 그 합성함수의 개수가 홀수(odd)일때 -1, 짝수(even)일때 +1을 갖는다. 그래서 예를 들어 바로 위의 사진에서, (13)(12)의 변환의 경우, even number이므로 sign은 1이라고 할 수 있다.
이 Cycle notation으로 Determinant를 적는 이유는, 그것이 굉장히 많은 대칭성(symmetry)을 띄기 때문이다. 어떤 좋은 성질이 있는지 알아보자
Properties of Determinant
Transpose와 determinant 는 독립적이다. \(det(A^T) = det(A) \)

Transpose란 column을 row와 exchange 해주는 일을 말한다. Transpose의 det와 원래 행렬의 det이 같다는 말은, 다시말하면 어떤 행렬의 row 의 linear independency와 col의 independency는 밀접한 관련이 있다는 말이된다. 증명은 위의 cycle notation으로 해도 되지만, 간단하게 3차원에서 확인해볼 수 있다.
Column Exchange 하면 부호가 음수가 붙는다.

Scailing 하면 k배 가되고, Addition 하면 변화가 없다.
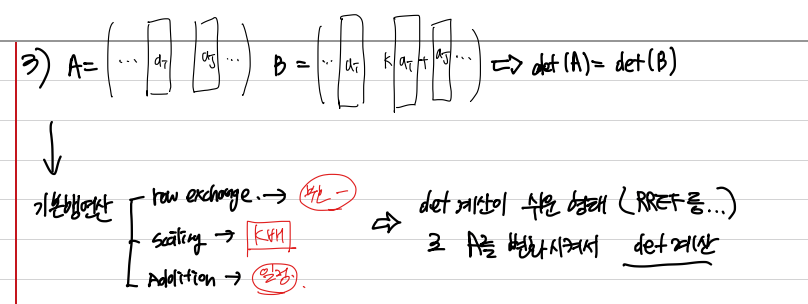
이로써, 세가지 기본행연산 과정에서 det 의 양상이 크게 변하지 않음을 알게 되었다.
두 행렬의 곱과 Determinant는 독립적이다. det(AB) = det(A) \(\times\) det(B)

이를 이용하면 어떤 행렬과 그 행렬의 역행렬의 곱이 기본행렬이므로, 전체에 행렬식을 씌우면 det(A)와 det(A^-1) 의 곱이 1이 됨을 알 수 있다. 여기서 알 수 있듯이, 어떤 행렬의 det가 0이 되면, 그 행렬은 역행렬을 가질 수 없다. 왜냐면 행렬식이 무한대인 행렬은 존재할 수 없기 때문이다.
How to apply these properties to calculation of a determinant
우리가 잠시 뒤에 다룰 Laplace Expansion에 더불어, EROs 의 determinant에 대한 대칭성이 유지되는 것을 활용하여, 어떤 행렬의 det를 구할때, 행렬식이 구하기 쉬워지는 form으로 행렬을 modify 해서 행렬을 구하면 좋다. 예를 들어 다음 경우는 네번째 Property를 활용해서 설명할 수 있다.
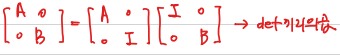
다음과 같은 상황에서 각각의 행렬식의 곱으로 계산할 수 있다. 이는 Laplace Expansion을 이용해서도 쉽게 구할 수 있다.
Inductive Calculation of Determinant
Determinant를 쉽게 계산하는 방식인 여인수 전개 (Laplace Expansion)에 대해 알아보자.
Laplace Expansion
어떤 한 행렬의 행렬식을 작은 단위로 나눠서 계산하는 방식이다.
Minor and Cofactor
(i,j) 번째 Minor란, 어떤 행렬의 (i,j) 성분에 대해, 그 행과 열을 제외한 남은 부분으로 만든 새로운 행렬의 행렬식을 의미한다.
Cofactor란, 그 Minor에 \( (-1)^{i+j}\)를 곱한 것을 말한다.
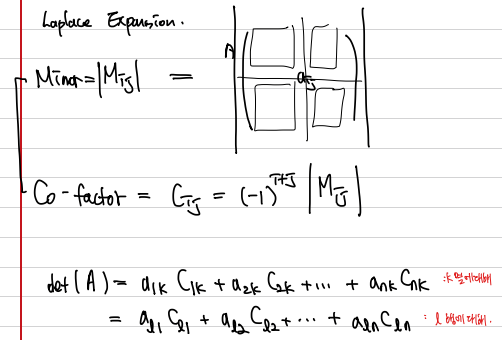
Calculation process
Minor와 Cofactor 를 이용하면, 행렬식을 아주 편하게 적을 수 있다. 하나의 행 또는 하나의 열에 대해 Laplace Expansion을 하면 행렬식을 구할 수 있고, 특히 0이 많은 행/열을 골라 그것에 대해 전개하면 훨씬 쉽게 계산할 수 있다.
Example) Determinant of Diagonal Matrix
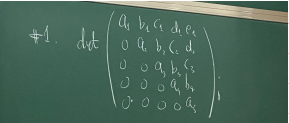
위와 같은 대각행렬의 행렬식은 대각 성분의 곱으로 정의된다. 그 이유는 첫번째 열에 대해 Laplace Expansion을 하면 그것의 첫번째 Cofactor를 구할 때 다시 Laplace expansion을 하게 되고, 이것이 inductive하게 일어난다.
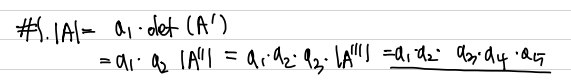
'Math > 선형대수학 Linear Algebra' 카테고리의 다른 글
| [4-2] Subspace, Linear combination, linearly independant (0) | 2023.03.23 |
|---|---|
| [4-1] Crammer's Rule, Adjoint, Vector Space (0) | 2023.03.20 |
| [3-1] Inverse Matrix (0) | 2023.03.13 |
| [2-1 , 2-2] Matrix (0) | 2023.03.12 |
| [1-1,1-2] Introduction to Linear Algebra (0) | 2023.03.06 |




댓글