목차
Crammer's Rule
설명
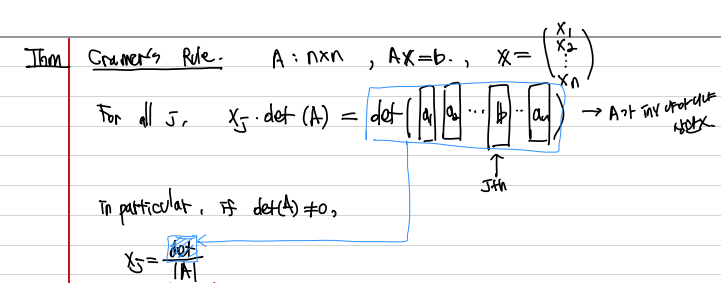
어떤 방정식 Ax = b에 대해서, 우리가 x의 j 번째 항이 궁금하다면, 아래를 계산하면 된다.
\[ x_j det(A) = det(A')\]
\( A' := \) j-th col is replaced with \(\vec(b)\) 여기서 det(A)가 0이 아니라면, 우리는 x_j를 구할 수 있다. 이는 다시말해 determinent가 0인 행렬은 역함수가 없다는 말과도 같다.
예시 문제
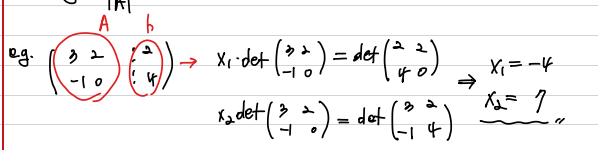
증명

EROs 들이 Determinent에 어떤 영향을 주는지를 숙지했다면 증명은 어렵지 않다. Ax 가 b와 같으므로, b를 Ax 로 치환한 후, A의 j번째 열에 대입한다. 대입된 Ax에서 j번째 성분을 제외한 나머지 항은 determinent의 값에 영향을 주지 못하므로 지워도 된다. 그러면 최종 determinent는 원래 det(A)에 x_j의 scala multiplication과 같다.
Adjoint (또는 Adjugate)
설명
Adjoint (Adjugate) 란, Cofactor matrix의 Transpose 이다. Adj에 대해 다음이 성립한다. \[Adj(A^T) = Adj(A)^T\]
이것이 왜 중요하냐면, Adjoint와 자기 자신의 곱은 항상 Identity Matrix에 상수 det(A)를 곱한것이 되기 때문이다. \[Adj(A) A = A Adj(A) = det(A) I_n\] 따라서, 만약 A가 역함수가 존재한다면 (Inversible) \[A^{-1} = \frac{Adj(A)}{det(A)}\]
눈여겨 보아야할 점은, 이것이 교환법칙이 성립한다는 점이다.
증명
A Adj(A) = det(A) I 증명 (우측 곱)

Adj의 jk 번째 성분은 Cofactor matrix의 kj번째 성분과 같다. 그러면 \[ A \cdot Adj(A)_{ij} = \sum A_{ik} C_{jk} \] 꼴이 된다. 여기서 j가 i와 같을 때는 Laplace Expansion이 되어 det(A)가 되지만, i와 j가 다르다면 이 값은 같은 row가 2개 있는 행렬의 determinant가 되어 값이 0이 된다.
j와 i가 다를 때 이것이 0이 되는 이유를 좀 더 자세히 설명하자면, 우리가 \(\sum a_{ik}C_{ik}\) 는 행렬 A의 det 라고한다. 이때 i 번째 열을 잡고, 각 성분에 대해 그 행과 열을 포함하지 않는 행렬의 남은 부분으로 Co factor를 잡는다. 그런데 만약에 Co factor를 i번째 열이 아닌 j번째 열을 기준으로 잡는다면, 그건 사실상 j번째 열에 i번째 열의 성분을 채워넣은 행렬의 행렬식을 계산하는 것과 마찬가지이다. 그렇게 된다면 두 행이 완벽하게 일치하는 행렬의 행렬식이므로, 그건 0이 된다.
Adj(A) A = det(A) I 증명 (좌측 곱)
\[ \left ( A Adj\left ( A \right ) \right )^T = \left ( det\left ( A \right ) I_n\right )^T = det\left ( A \right ) I_n \]
인데, transpose를 취해주면 앞뒤 순서 바뀌므로, \[ Adj(A)^T A^T= det\left ( A \right ) I_n\] 이다.
그런데 우리는 위의 Determinant의 성질에서 \[ Adj(A)^T = Adj(A^T)\]
이므로, \[ Adj(A^T) A^T = det(A) I_n \] 이다. A의 Transpose를 새로운 행렬 B로 잡으면, Adj의 좌측곱도 증명이 된다.
Vector Space
우리가 고등학교에서 벡터를 배울때는 "크기와 방향을 가진 물리량"이라 배웠고, 화살표에 대응시켜 여러 계산을 했다. 화살표는 일상적인 상황에서 벡터의 개념을 형상화하는데 좋은 도구이다. 그러나 우리가 수학 또는 물리학에서 벡터를 다룰 때는 일상적 영역에서의 벡터의 개념을 확장시켜, 더 이상 화살표로는 설명하기 어려운 상황을 마주한다.
우리는 앞으로 벡터를 새롭게 정의할 것이다. 벡터가 만족하는 여러 성질, 기준을 정하고, 그것을 만족하는 집합을 벡터 공간이라 부를 것이다. 그리고 그 공간을 이루는 각 원소를 벡터라 부른다. 그것이 비록 우리가 지금껏 다뤄왔던 화살표와는 거리가 있을지라도, 수학적으로 벡터라 정의하고 동일하게 다룰 것이다.
Set , Addition, Scala Mutiplication
우리가 어떤 집합이 Vector Space인지를 판단하기 위해서는 3가지를 알아야한다. (1)Set (2)Addition (3)Scala Multiplication 이 세가지가 그 공간에서 어떻게 정의되는지를 알아야한다. 이게 무슨 생뚱맞은 소리인가 반문할 수도 있다. 덧셈이 그냥 덧셈이지, 상수곱이 그냥 상수곱이지 어떻게 정의되느냐가 무슨 의미가 있냐고 물을 수 있다. 그러나 그건 우리가 관용적으로 자주 사용하던 벡터공간의 법칙에 너무 적응한 탓이고, 연산을 새롭게 정의해주면, 그건 다른 공간이 될 수 있다. 예를 들어, 우리가 벡터 (a,b)와 벡터 (c,d)를 더할때, 어떻게 더하는가는 우리가 정해주기 나름이다. \[ \left ( a,b \right ) + \left ( c,d \right ) = \left ( a+c, b+d \right )\] 가 성립함은 너무도 당연하지만, 사실 이건 우리가 이 벡터공간을 만들어주기위해 임의로 정한것이다. 덧셈을 다르게 정의하면 이 집합은 벡터공간이 되지 않을 수도 있다. 예를 들어 \[ \left ( a,b \right ) + \left ( c,d \right ) = \left ( a-c, b-d \right )\] 이렇게 정의해주면 후술될 여러 조건을 만족시키지 못한다. 상수곱도 마찬가지이다. 우리는 상수곱을 각 성분에 상수를 곱하는 것으로 정의했다.\[ k \left ( a,b \right ) = \left ( ka,kb \right ) \] 하지만 이 역시도 우리가 다르게 정의해줄 수 있는것이다. 그러나 그것이 벡터공간이 될지는 장담할 수 없다.
정리하자면, 우리가 어떤 집합이 벡터공간인지를 알기 위해선, 집합뿐만 아니라, 그 집합의 원소사이에 덧셈이 어떻게 정의되느냐, 상수곱이 어떻게 정의되느냐 까지 포함하여, 그것이 벡터공간의 조건을 만족시킨다면 그 연산자를 포함한 전체 집합을 벡터공간이라 부르고, 그 집합의 원소들을 벡터라 부른다.
만족해야하는 조건들

첫번째는 덧셈이다. 집합에 소속되어있는 두 원소의 덧셈 결과가 다시 그 집합의 원소가 된다.
두번째는 덧셈에 대한 교환법칙(Commutitive)이다.
세번째는 덧셈에 대한 결합법칙(Additive)이다.
네번째는 덧셈에 대한 항등원이 존재한다.
다섯번째는 덧셈에 대한 역원이 존재한다.
여섯번째는 상수곱한 원소가 다시 그 집합의 원소가 된다.
일곱번째는 두 원소의 합의 상수곱에 대해 분배법칙(Distribution)이 성립한다.
여덟번째, 두 상수의 합이 한 원소에 곱해질때, 분배법칙이 성립한다.
아홉번째, 상수곱에 대한 결합법칙이 성립한다.
마지막 열번째, 곱셈의 항등원이 되는 상수가 존재한다.
a set of matrix , polynomials, all continous functions which are vector spaces
행렬

가로세로 길이가 n인 모든 원소가 실수인 행렬의 전체 집합 \( M_{n \times n}(\mathbb{R}) \) 이 있다. 이게 벡터공간이냐 물으면, 우선 덧셈과 상수배가 어떻게 정의되냐라고 반문해야한다. 일반적인 덧셈과 상수곱으로 정의된다면, 위의 열가지 조건을 만족시킨다. 따라서 벡터공간 ~!
다항식

최고차항의 차수가 n보다 작거나 같고 모든 계수가 K 집합(실수, 허수, 복소수, 유리수 등등)의 원소인 Polynomial의 집합이 있다. 이 역시 덧셈과 상수곱이 관습적으로 정의된 것과 같다면 벡터공간이다. 그러나! 만약 최고차항의 차수가 n인 다항식의 집합이라면 벡터공간이 아니게 된다. 왜냐면 어떻게 잘 빼면 최고차항의 차수가 낮아지기 때문이다.
함수

마지막으로 어떤 구간 [a,b] 정의된 모든 연속함수의 집합에 대해, 덧셈과 상수곱이 우리가 알던대로 정의된다면 벡터공간이다. 항등원은 y=0 상수함수이고, 역원은 x 축 대칭함수이다.
'Math > 선형대수학 Linear Algebra' 카테고리의 다른 글
| [4-2] Subspace, Linear combination, linearly independant (0) | 2023.03.23 |
|---|---|
| 3-2 Determinant (0) | 2023.03.16 |
| [3-1] Inverse Matrix (0) | 2023.03.13 |
| [2-1 , 2-2] Matrix (0) | 2023.03.12 |
| [1-1,1-2] Introduction to Linear Algebra (0) | 2023.03.06 |




댓글