목차
슈뢰딩거 방정식을 풀어서 일반해 \(\Psi(x,t)\) (General solution)을 구하는 방법
What we can solve in QM
우리가 양자역학에서 완벽하게 풀수있는 문제는 고작 세개밖에 되지 않는다.
- 첫번째, 무한 퍼텐셜 우물 (Infinite potential well)
- 두번째, Harmonic oscillator
- 세번째, Hydrogen atom
앞으로 세가지에 대해 배워볼 것이다. 우선 그에 앞서 일반적으로 슈뢰딩거 방정식을 푸는 과정을 들여다보자.
변수분리법 .Separation of variables
변수분리법을 이용해 위치에 대한 식과 시간에 대한 식으로 해를 쪼개서 풀것이다.
모든 미분방정식이 변수분리법으로 풀리는 것은 아니지만, 슈뢰딩거 방정식은 효과적으로 풀리며, 또 이 방식은 미분방정식에 접근할때 물리학자들이 가장 선호하는 방식이다. 특수한 가정을 토대로 접근해 얻은 해를 선형결합하여 일반해를 구할 수 있다.
변수 분리법이 적용된다는 것은 Coefficient C_n이 Time independant 함을 의미한다. 다시말해, 시간이 흘러도 각 State의 probability mass function이 일정하다는 의미이다. 대부분의 경우에 계수 C_n은 Initial Condition에 의해 결정되는 constant지만, 만약 시간에 따라 변하는 경우 Method of Perterbation 이나 Numerical Method를 써야한다고 하는데, 그게 뭔지는 아직 잘 모르겠다.
그러나 대부분의 양자역학 문제는 변수 분리법의 적용으로 풀 수 있고, 이만해도 내 수준에선 충분히 어렵다. 변수 분리법은 특히 위치와 시간이 서로 영향을 주지 않는 두 함수로 구분되어 있어 각 함수가 편미분이 아닌 상미분으로 분리가 되어 쉽게 해결할 수 있다.
How to solve 1 Dim Time Dependent Schrodinger Equation (1D-TDSE)
우리가 Time dependant equation의 General solution을 구하려고할 때, 한번에 구할 수 없다. t=0일때의 해(Initial condition)을 참고하여 TI 방정식의 solution과 선형결합의 계수 c_n 구한다. 앞서 말했듯 C_n 은 시간에 무관(한 경우에만 변수분리법을 쓸 수 있으므로)하므로, Initial condition으로 얻은 값을 그대로 general solution에 적용할 수 있다.
\[ i \hbar \frac{\partial}{\partial t}\Psi(x,t) = -\frac{\hbar^2}{2m}\frac{\partial ^2}{\partial x^2}\Psi(x,t) + V \Psi(x,t) \]
파동함수 일반해는 위치와 시간에 대한 함수이다. 이것을 위치에 대한 함수와 시간에 대한 함수의 곱으로 나타내보자. 이때 지금까지는 \( \psi , \Psi \) 를 구별없이 남용했지만, 앞으로는 엄밀하게 사용할 것이다. 소문자는 오직 x에 대한 함수이고, 대문자는 x와 t에 대한 함수이다.
$$\Psi_n ( x,t) = \psi_n (x) \phi_n (t)$$
그런다음 슈뢰딩거 방정식에 대입한다.
\[ i \hbar \frac{\partial}{\partial t}\psi_n (x) \phi_n (t) = -\frac{\hbar^2}{2m}\frac{\partial ^2}{\partial x^2}\psi_n (x) \phi_n (t) + V \psi_n (x) \phi_n (t) \]
이때 변수가 분리되었으므로 두 편미분은 각각에 대한 상미분으로 바꿀 수 있고, 양변을 $\psi (x) \phi (t)$ 로 나눠준 뒤 x에 대한 식과 t에 대한 식을 각각 우변과 좌변에 모아준다. 여기서 중요한 점은, 우리는 시간에 대해 불변인 퍼텐셜만 다룬다는 점이다! (참으로 가정을 많이 한다. 언제쯤 일반적인 물리학을 할 수 있을까 )
\[ i \hbar \frac{\frac{d \phi}{dt}}{\phi} = -\frac{\hbar^2}{2m}\frac{\frac{d^2 \psi}{dx^2}}{\psi} + V \]
좌변은 시간에 대한 함수이고 우변은 위치에 대한 함수인데, 이 두개가 임의의 t와 x에 대해 항상 성립하는 항등식이라면, 이는 저 식이 "상수" 임을 의미한다.이게 무슨 말이냐면, 만약 저 값이 상수가 아니라, t 또는 x의 값에 따라 달라지는 값이라고하자.만약 t를 그대로 둔 채로 x를 바꿔준다면, 좌변에서 보면 함수값은 그대로여야 하는데, 우변에서 보면 식의 값이 바뀌어야 한다. 모순이라는 말!따라서 위의 식은 t와 x에 대해서 무관한 상수가 나오는 항등식이다! (이 논리를 완벽히 이해하고 넘어가야 한다.)
\[i \hbar \frac{\frac{d \phi}{dt}}{\phi} = -\frac{\hbar^2}{2m}\frac{\frac{d^2 \psi}{dx^2}}{\psi} + V = E\]
그러면 우리는 A = B = E 꼴의 식을 얻었으므로, A = E , B = E 꼴의 두 방정식으로 분리할 수 있다.
\[ i \hbar \frac{\frac{d \phi}{dt}}{\phi} = E\]
\[ -\frac{\hbar^2}{2m}\frac{\frac{d^2 \psi}{dx^2}}{\psi} + V = E \]
시간에 대한 방정식 (Time)
첫번째로 시간에 대한 식이다.
\[ i \hbar \frac{\frac{d \phi}{dt}}{\phi} = E\]
위의 식은 쉽게 풀 수 있다. dt를 넘기고 양변을 적분하면 ln 이 나오는데 그걸 지수로 옮겨 적어주면 아래의 해가 나온다.
\[ \phi_n(t) = e^{\frac{-iE_nt}{\hbar}} \]
위치에 대한 방정식 (Displacement) - 1D Time Independant S.E.
그 다음 위치에 대한 식을 보면
\[ -\frac{\hbar^2}{2m}\frac{\frac{d^2 \psi_n}{dx^2}}{\psi_n} + V(x) = E_n \]
여기서 양변에 \( \psi_n \) 를 곱해주면
\[ -\frac{\hbar^2}{2m}\frac{d^2 \psi_n(x)}{dx^2} + V\psi(x) = E\psi_n(x) \]
가 나오고 , 이 식을 시간독립 1차 슈뢰딩거 방정식 (1-dim T-I S.E.)라고 부른다. 줄여서 1DTI SE라고도 부른다.
이 방정식의 해를 구하면, 유일한 해가 아니라, \( \psi_1, \psi_2,...,\psi_n \) 의 수많은 "시간 독립" 해가 나온다.
각각의 해에 대해서 우리는 $E_1, E_2,...,E_n$ 를 구할 수 있다. (\(\psi\)가 결정되면 E가 결정된다.) 그러면 각각에 대해 $\phi_n(t) = e^{\frac{-iE_nt}{\hbar}}$를 계산할 수 있으므로, 각각의 $\Psi_n(x,t)$를 구할 수 있다!
$$\Psi_n(x,t) = \psi_n(x)\phi_n(t) =\psi_n(x) e^{\frac{-iE_nt}{\hbar}}$$
이때 이 $\Psi_n(x,t)$ 를 "변수분리 가능한 해(Seperable Solution)"라고 부른다. 그 이유는 각각이 변수분리되는 해이기 때문이다. 일반적인 Time dependant 슈뢰딩거 방정식의 general solution은 Seperable solution들의 선형결합으로 이루어진다. 그때 선형결합의 계수 \( c_n\) 은 후에 다시 배우겠지만, 그것의 제곱은 각 State의 Probability Mass function이 된다.
\[ \Psi(x,t) = \sum c_n \Psi_n(x,t) = \sum c_n \psi_n(x) \phi_n(t)\]
Seperable Solution에게는 세가지 특징이 있다
또한 TI SE의 해는 유일한 것이 아니라 굉장히 많고, TD SE의 일반해는 이런 TI SE의 해의 선형결합으로 이루어진다.
\[\Psi(x,t) = \sum c_n \Psi_n(x,t) = \sum c_n \psi_n(x) \phi_n(t)\]
시간에 대해 Stationary state 를 갖는다.
일반해는 time dependant 하지만, 확률밀도는 time independant 하다. 이것은 Time independency와는 다른 개념이다. (Stationary doesn't mean that the system is time independant) Stationary란, 파동함수 자체는 time dependent 할지라도, 그것의 확률밀도\(|\Psi|^2\)나 에너지\( E_n\)가 time independant 함을 의미한다. 이는 파동함수의 시간 텀이 exp(imaginary) 꼴이라, 파동함수를 제곱하는 과정에서 Conjugate와 곱해지며 지수법칙에 의해 1로 사라지기 때문이다.

기댓값은 오퍼레이션이 거의 대부분 time independant하므로 기댓값도 계산해보면 시간텀이 변수분리법으로 쪼개면 컨쥬게이트와 지수법칙에 의해 상쇄되므로 time independant 하다.
Definite total energy 에너지가 하나로 결정된다.

또한 에너지가 하나의 값으로 정해져 있다. (state of definite total energy) 사실 이건 첫번째 성질의 동어반복이다. Stationary하기 때문에, 헤밀토니안 연산자를 취해 에너지를 구하면 E_n이 나온다. 그 이유는 시간 독립항에 대해 헤밀토니안의 standard deviation을 구하면 0이 나오니 때문이다. 위의 계산에서 두개의 헤밀토니안이 연속으로 작용하여 E의 제곱을 내뱉는 과정은 아래와 같이 설명된다. \[ \int\Psi^*\hat{H}\hat{H}\Psi dx=\int\Psi^*\hat{H}E\Psi dx=E\int\Psi^*E\Psi dx=E^2\int\Psi^*\Psi dx=E^2\]
General Solution is the linear combination of separable solutions
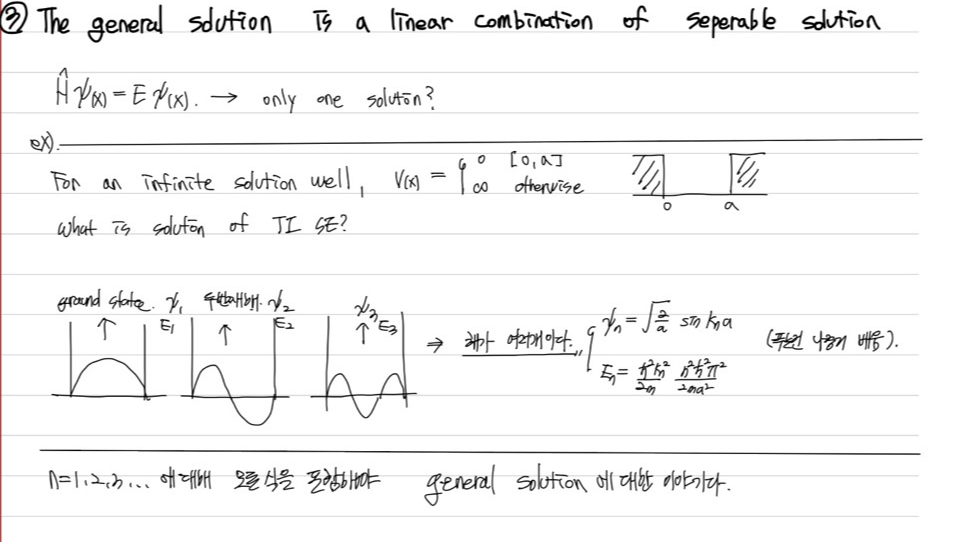
가장 간단한 infinite potential well을 생각했을때, 우리는 해가 정말 다양하게 나오는 걸 알수 있다.
그래서 Genearal solution을 나타내면 $$\Psi(x,t) = \sum c_n \Psi_{n}(x,t) = \sum c_n \psi_{n} \phi_{n}$$ 여기서 c_n은 Initial condition으로 구한다.만약 우리가 SE의 시간독립해를 구했다면 우리는 TD SE의 일반해까지 알 수있다는 말이된다. 왜냐면 시간 독립항 해를 이용해 시간 항 지수꼴까지 구할 수 있기 때문이다.

양자역학 문제 국룰
QM의 문제는 아래 둘 중 하나로 나온다
1. 퍼텐셜 V가 주어진다. 이걸 받으면 우린 운동에너지 K의 식도 알고 있으므로, 사실상 헤밀토니안 연산자를 아는 것과 같다. TI-SE 은 다시쓰면 \( \hat{H} \Psi = E \Psi\) 와 같다. 다시말해, V를 받은건 TI-SE를 받은것과 같다.
2. t=0일때의 Initial condition이 주어진다. \( \Psi(x,0)\)가 주어졌다는 말이다. 이걸로 무엇을 할 수 있는가? 바로 계수 \( c_n\)을 구할 수 있다. Orthogonal condition을 이용하여 양변을 \( \psi_n^*\)를 곱해주고 적분하면 계수를 구할 수 있다. 방금설명한 내용은 다음 글에서 더욱 자세히 다루겠다.

문제 푸는 프로세스
그렇다면 우린 아래 순서대로 문제를 풀면 된다.
- TI SE를 푼다.
- 시간 독립 해를 N에 대한 식으로 구한다. 그리고 E도 n에 대한 식으로 구한다.
- 2에서 구한 것들을 선형결합해서 일반해를 나타낸다.
- 초기 조건을 이용해 t=0으로 계수를 구한다.
보통 초기조건은 완벽하게 주어지지 않고 미지수 A등을 섞어서 주기때문에 이 A의 값을 알아내야한다. 이것은 Normalization condition을 이용해 계산해준다. 이렇게 초기조건을 얻었다면, 문제상황에 맞게 (Infinite potential well 이나 harmonic oscillation 등) 잘 알고있는 파동함수를 잡아준다. (이렇게 우리가 잘 아는 문제에 대해선 위에서 서술한 1~3과정을 skip할 수 있다.) 이후 Orthogonality Condition을 이용해 Initial condition을 이용해 계수를 결정해준다.
다음 시간엔 Infinite potential well 에 대해 배워보자
'Physics > 양자역학 Quantum Mechanics' 카테고리의 다른 글
| Single photon Interference (0) | 2023.05.29 |
|---|---|
| [4-2] Harmonic Oscillator in QM (Algebraic Method) (0) | 2023.03.23 |
| [4-1] Infinite potential well (2) (0) | 2023.03.23 |
| 3-2 Infinite potential well (0) | 2023.03.16 |
| [2-2] 운동량 연산자 유도하기, 불확정성 원리, 슈뢰딩거 방정식 유도 (0) | 2023.03.14 |
| [1-1,1-2] 양자역학의 시작 (2) | 2023.02.28 |




댓글