[1-1,1-2] 양자역학의 시작

목차

Classical Mechanics VS Quantum Mechanics 고전역학 대 양자역학 

Classical mechanics 고전역학

Purpose : 시간에 따른 물체의 위치 \(chi\left ( t \right )\) 를 찾는다. 위치를 알면 속도(위치의 시간미분) , 가속도(속도의 시간미분) 운동량 (속도와 질량의 곱) 운동에너지(1/2*질량과 속도제곱의 곱)

How : Newton's Second Law \(F = ma\)

---

Quantum Mechanics 양자역학

Purpose : 파동함수 \(Psi\left(t \right)\)를 구한다. 

How : Schrodinger' Equation \(i\hbar\frac{\partial \Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2\Psi}{\partial t^2}+V\Psi\) 를 푼다. 

---

Schrödinger equation and wave function 슈뢰딩거 방정식과 파동함수 

슈뢰딩거 방정식을 본격적으로 배우기에 앞서 몇가지 특징점들을 알아보자. 슈뢰딩거 방정식의 근인 파동함수는 실수인가 허수인가, 슈뢰딩거 방정식은 선형인가 비선형인가. 그리고 파동함수의 의미는 무엇인가. 

 $\Psi$ is real or imaginary? 파동함수는 실수인가 허수인가

\(\Psi = \left | \Psi \right |e^{i\phi}\) 이다. 이때 앞의 절댓값은 파동함수의 크기 magnitude이고, 뒤의  exp 항은 파동함수의 Phase 를 나타낸다. 

오일러 공식 \(e^{i\phi} = cos(\phi) + i sin(\phi)\) 에 의해 파동함수는 허수부와 실수부를 갖게 되는데, 이로써 파동함수는 복소수임을 알 수 있다. 

---

Schrödinger Eq is linear 슈뢰딩거 방정식의 선형성 + 2.4. Normalization(정규화)

슈뢰딩거 방정식의 한 근 $\psi_1$ 과 $\psi_2$ 가 있다. 이 두  Psi는 각각 \(i\hbar\frac{\partial \Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2\Psi}{\partial t^2}+V\Psi\)  를 만족하므로, 두 식을 상수배 후 더해서 나오는 새로운 방정식의 근은, 두 파동함수의 선형결합인 \(\psi_3 = a\psi + b\psi\)이다. 즉, 슈뢰딩거 방정식은 선형이다. 

(맥스웰 방정식도  선형이다. 대표적으로  Gauss's law \(\nabla \cdot E = \frac{ \rho}{\epsilon_0}\) 의 두근을 \(E_1, E_2\)로 잡고 두 방정식을 더하면 새로운 전기장 \(E_{tot} = E_1 + E_2\)에 대해서 전하밀도 \(\rho_{tot} = \rho_1 + \rho_2\)를 만족한다. 즉 linear하다. 

그러나 Newton's 2nd law  $F=ma$ 는 F에 따라서 선형성이 다르다. 예를 들어 Hooke's law 1차항  F = -kx 에 대해서는 선형이지만, minor terms 를 고려하면 비선형이 된다. )

---

규격화 조건 ( Normalization) 

그러나 슈뢰딩거 방정식이 선형적이라고 해서, 근의 선형결합 모두가 물리학적으로 허용되는 것은 아니다. 슈뢰딩거 방정식의 근은 "정규화(확률밀도의 전구간 적분값은 1이다)"라는 조건을 만족시킬 때 비로소 근이된다. 

예를 들어 \(\Psi = Ax\) 를 슈뢰딩거 방정식에 대입해보면 방정식을 만족한다는 것을 알 수있다. 그러나 이 파동함수(?)는 물리학적으로 허용되는 근이 아니다. 왜냐하면 파동함수의 제곱(확률밀도)의 전구간 적분이 1이 아니기 때문이다. (양의 무한대 발산) 

\(\psi\)가 근일 때, \(a\psi\)의 파동함수의 적분값이 1이 되기 위해서는 앞에 곱해지는 상수a가 다음 조건을 만족 시켜야 한다. 

\[\left | a \right | = 1\]

여기서 고등학생처럼  \(a = \pm 1 \) 하면 안된다. (내가 그랬다.) 우리는 a를 복소수까지 확장했으므로, 복소수의 크기가 1인 경우를 생각해야 한다. 복소 평면에서 원점으로부터 거리가 1만큼 떨어져있는 점을 가리키는 벡터... 바로 단위원 \(e^{i\phi}\)이다. 이때 \(\phi\)는 실수이다. 그 이유는 \(e^{i\phi}\) 의 크기를 구하기 위해 그의 켤레 복소수(컨쥬게이트) \(e^{-i\phi}\) 와의 곱 \(e^{i\phi-i\phi} = e^0 = 1\) 이 1로 나오기 때문이다. 실수가 아니라 복소수라면 켤레복소수의 꼴은 달라지고 크기는 1이 되지 않는다. 

---

좋은 근의 조건 : 슈뢰딩거 방정식 만족 / 정규화 / + \(\alpha\)

좋은 근이란 슈뢰딩거 방정식을 만족하면서 규격화 조건을 만족시키는 근이라는 것을 알게 되었다. 

우리는 또 하나 좋은 근의 필요 조건을 구할 수 있는데, 바로 \( \lim_{x \to \infty} \psi \to 0 ... faster than \frac{1}{\sqrt{x}}\) 이다. \(\frac{1}{\sqrt{x}}\) 보다 0으로 더 빠르게 수렴해야함을 의미하는데, 그 이유는 다음과 같다. 아래의 법칙이 성립한다.

 

\[\int_{-\infty}^{+\infty}\left|\Psi\right|^2 dx = 1 \Rightarrow  \lim_{x \to \infty}\left|\Psi\right|^2 dx \to0\] 이다. 이는 어떤 무한급수가 수렴하면 일반항의 극한값은 0이된다는 정리로부터 유도되었다. (적분은 급수의 확장이니) 

다시말해 \(\left|\Psi\right|^2 dx \to0\) 이고, x 가 무한대로 가면 \(dx \to x\) 이므로(교수님께서 이렇게 설명하셨는데, 오류가 있는 것 같다.), \(\Psi^2$ 이 $\frac{1}{x}\)보다 빠르게 수렴해야한다.  \(\frac{1}{\sqrt{x}}\) 보다 0으로 더 빠르게 수렴해야한다.

---

t=0 일때 x에 대해서 정규화 된다는 것은 알겠는데, 시간이 바뀌면 적분값이 달라질 수 있지 않을까? 

결론부터 말하자면 아니다. \(\int_{-\infty}^{+\infty}\left|\Psi\right|^2 dx\) 값은 시간에 대해 언제나 일정하다. 다시 말해, 

\[\frac{\partial \int_{-\infty}^{+\infty}\left|\Psi\right|^2 dx}{\partial t} = 0\] 임을 증명할 수 있다. 

확률밀도의 전구간 적분값은 시간과 무관하게 일정하다는 증명

---

Loss of determinism 파동함수의 확률론적 해석 (코펜하겐) 

20세기 물리학계의 가장 논쟁적인 주제였던 파동함수의 해석, 즉 어떻게 입자를 파동함수로 묘사할 수있는가? 에 대하여 세가지 해석이 당시에 존재했다. 

첫번째는 현실주의자(the realist)이다. 아인슈타인이 대표하는 이 현실주의자들은 어떤 위치 C에 입자가 존재할 확률만을 나타내는 파동함수는 "정보가 부족한 상태"라고 생각했다. 그들은 우리가 아직 알지 못하는 어떤 "숨은 변수(Hidden variable)"가 있어서, 이것을 우리가 알면  C라는 위치에 입자가 존재할 확률이 100%로 나올 것이라 생각했다. 이들에 따르면 양자역학은 불완전한 이론이었다. 이들은 어떤 위치에서 발견된 입자는 측정 이전에도 그 위치에 존재했을 것이라고 주장한다. 

두번째는 정통주의자(The orthodox)이다. 막스 보른과 닐스 보어가 대표하는 정통주의자들은 숨은 변수 따위는 없고, 우리가 알 수 있는 것은 주어진 시간과 위치에서 입자의 존재 확률뿐이라고 말한다. (Even if you know all about the theory, but still you cannot predict with cerntainty where the particle is.) 이들은 파동함수와 그의 켤레복소수의 곱인 \(\psi * \psi^* = \left | \psi \right |^2 = \rho (x,t)= $probability density\) : 주어진 위치/시간에 입자가 존재할 확률(밀도)이다. 연속확률이므로 한점에서의 확률은 의미가 없고,일정 구간내에서의 정적분의 값으로 확률을 나타낸다. 

세번째는 불가지론자(The agonist)이다. 이 논의 자체가 의미없다고 말하는 것인데, 당시 대부분의 물리학자들은 이에 속했다. 

한세기가 지난후 정통주의자(두번째)의 입장이 옳다는 것이 밝혀졌다. (2022 노벨 물리학상 벨 부등식 위배실험) 

---

Superpostion in Q.M. 

우리는 Electro statistics, dynamics 에서 전기장 E field 가 superposition 됨을 수도 없이 관찰했다. 양자역학의 파동함수 역시 중첩되는데, 파동함수가 중첩된다는게 물리학적으로 어떤 의미를 갖는가? 

\[\Psi = a\Psi_1 + b\Psi_2\]

<Mach-Zehnder interferometer 마하 젠더 간섭계>

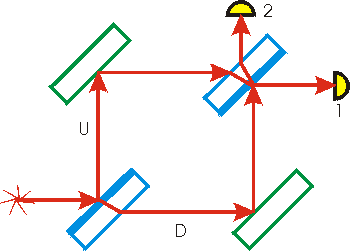
위 장치에서 Beam splitter에서 쪼개 진 빛이 각 mirror 1,2에서 반사된 뒤 다 시 beam splitter로 들어와 두개의 검출기 D0와 D1에 도달한다. 이때 두개의 path length를 미세하게 조정하여 한쪽에서는 보강간섭을, 한쪽에서는 상쇄간섭을 일어나게 할 수있다. 

놀라운 점은 위의 실험을 광자 한 개 단위로 할 때도 같은 현상이 관찰된다는 점이다. 즉 광자는 스스로와 간섭한다. (It interferes with its own)

광자 한개에 대하여 D0에서 검출될 때의 상태를 $| A \rangle $ D1에서 검출될 때의 상태를 $|B \rangle$ 이라 하면 전체 파동함수는 

\[ | \Psi \rangle = a | A \rangle + b | B \rangle\]

이다. 이때 a와 b는 각각 D0와 D1이 일어날 확률(비)을 의미한다(정규화 되기 전). 

(이때 \( | \rangle\) 요렇게 생긴 걸 Ket이라 하고, 이는 벡터를 의미하는 표시이다. \(\langle |\)을 Bra라고 하고, 이는 선형함수를 의미한다. 이 표현 방식을 Bra-ket notation 혹은 Dirac notation이라고 부른다.)

이때 전체 확률은 1이 되어야 하므로, 위 파동함수의 확률은 1이 되어야한다. (정규화) 이에 따라서 A의 확률을 다시 구해 보자면 \[ P_A = \frac{a^2}{a^2+b^2}\] 이다. 이때 분모에 왜 2ab항이 없냐고 생각할 수 있는데, Ket은 벡터로서 D0와 D1의 내적은 0 (orthogonal)이기 때문에 2ab항이 없다. 

우리가 또한 알 수 있는것은 하나의  State앞에 어떤 상수가 곱해져 있든, 그것은 아무 의미가 없다는 점이다. 결국 Normalize하면 같은  State가 되므로 $10|\Psi \rangle , 10^5|\Psi \rangle$ 모두 같은  State이다. 

---

Physical Quantity

고전역학에서 우리가 어떤 물체의 위치 X(t)에 대해 얘기하는 것은 어렵지 않다. 하지만 양자역학에서 우리는 입자에 대해 파동함수의 분포만 알 수 있다. 이에 따라 우리는 물체의 정확한 위치가 아닌, 물체 위치의 기댓값을 계산할 수 있다. 

우리 각자에게는 속을 들여다 볼 수 없는 상자 하나씩 있고, 그 속에는 구슬 하나씩 들어있다. 상자 속 구슬의 위치는 완벽히 무작위다. 개별 구슬의 정확한 위치를 알 수는 없지만, 우리가 모두 상자속 구슬의 위치를 확인한 뒤, 그것의 평균을 구한다면 상자의 중심부가 그 평균에 가까워진다는 것을 알 수 있다.  중요한 것은, 우리는 하나의 상자를 여러번 들여다 보는 것이 아니라, 수많은 상자를 각각 측정한 뒤 평균을 낸다는 점이다. 하나의 상자를 여러번 측정해봤자, 항상 같은 위치에 구슬이 있을 것이다. 

이때의 위치의 기댓값을

\[ \left \langle x \right \rangle = \int_{-\infty}^{\infty}x\left | \Psi \right |^2dx\]

라고 한다. 이 위치의 기댓값을 미분하면 속도의 기댓값도 구할 수 있다. 

\[\frac{\partial \left \langle x \right \rangle}{\partial t}= \int_{-\infty}^{\infty}x\frac{\partial }{\partial t}\left | \Psi \right |^2dx\]

위와 같이 부분적분을 사용해 이를 정리하면 다음 식을 얻을 수 있다.

\[\frac{\partial \left \langle x \right \rangle}{\partial t}= - \frac{i \hbar}{m}\int\Psi^*\frac{\partial \Psi}{\partial x}dx\]

하지만 양자역학에선 관습적으로 속도보다 운동량을 많이 사용한다. 

\[\left \langle p \right \rangle = m\frac{\partial \left \langle x \right \rangle}{\partial t}= - i \hbar\int\Psi^*\frac{\partial \Psi}{\partial x}dx\]

이제 위의 두식을 보기 좋게 정리하자면

\[\left \langle x \right \rangle = \int \Psi^* (x) \Psi dx\]

\[\left \langle p \right \rangle = \int \Psi^* (\frac{\hbar}{i}\frac{\partial }{\partial x}) \Psi dx\]

이때 위의 x를 위치 x의 "연산자"라고 부르고, 연산자 x가 위치를 표현한다고 이야기한다. \( \left \langle \hat{x} \right \rangle = x \)

또한 위의 $\frac{\hbar}{i}$ 는 운동량 p의 연산자라고 부르고, 연산자 \(\left \langle \hat{p} \right \rangle\)가 운동량을 표현한다고 이야기 한다. \(\left \langle \hat{p} \right \rangle = \frac{\hbar}{i}\frac{\partial }{\partial x}\)

 

나머지는 다음 시간에

양자역학 필기노트.pdf

11.81MB