[2-1/2-2] Discrete Distribution, pmf, moment, mgf

목차

Discrete Random Variable and Probability Distribution 이산확률변수와 확률 분포 

현실 세계의 사건에 대해 확률을 계산하기 위해서는, 언어적이고 추상적인 사건을 구체적인 숫자에 대응시킬 무언가가 꼭 필요하다. 다시말해 사건 A가 일어날 확률을 계산하려면, 모든 사건은 일정한 규칙에 따라 각각 하나의 실수에 대응되어야 한다. 확률변수 X (Random variable) 란, 사건 A 에 대하여 임의의 실수 하나를 대응시켜주는 real-valued function을 의미한다. 

사건 A가 일어날 확률은, 사건A에 대응되는 실수 X(A)가 집합 B에 포함될 확률로 구한다. $$P\left ( X\in B \right ) = P\left [ \left\{ \ s \in S : X(s) \in B\right\} \right ]$$

Discrete random variable 이산확률변수 

X의 range가 countable 일때. 확률변수가 대응시킨 실수들이 셀수 있을때 (finite or infinitely countable) 

Indicator function 

$$I(x \in A) = I_A (x) = \begin{cases}
 1& \text{for } x \in A \\ 
 0& \text{otherwise } 
\end{cases}$$

(갑자기?) Maclaurin Series 

매클로린 시리즈는 0에서 정의된 테일러 시리즈이다. 

Taylor Series : \(g(y) = \sum_{i=0}^{\infty}\frac{g^n(a)}{n!}(y-a)^n\)

Maclaurin Series : \(g(y) = \sum_{i=0}^{\infty}\frac{g^n(0)}{n!}y^n\)

매클로린 시리즈의 수렴구간은 비판정법에 의해 결정된다.\( |y| < \frac{1}{K} $ 여기서 $K = \lim_{x \to \infty}\frac{a_{n+1}}{a_n}\)  이다. 

첫번째로, 지수함수 Exp(x)의 매클로린 급수는 아래와 같다. 

$$e^y =  \sum_{i=0}^{\infty}\frac{g^n(0)}{n!}y^n =  \sum_{i=0}^{\infty}\frac{y^n}{n!}$$

\(g^n(0) = 1 \)이기 때문이다. 수렴구간은 실수 전 집합이다. 

다음은 Geometric Series 이다.

$$\frac{1}{(1-y)} =  \sum_{i=0}^{\infty}\frac{g^n(0)}{n!}y^n =  \sum_{i=0}^{\infty}y^n$$

\(g^n(0) = n! \) 이기때문에 아래 n!과 약분이 된다. 이 경우에 수렴구간은 \(|y| <1\)이다. 

마지막으로, Negative Binomial Series이다.  

$$\frac{1}{(1-y)^r} =  \sum_{i=0}^{\infty}\frac{g^n(0)}{n!}y^n =  \sum_{i=0}^{\infty}\binom{n+r-1}{n}y^n$$

이 경우엔 \(g^n(0) = \frac{(n+r-1)!}{(r-1)!}\) 인데, 아래에 있는 n! 과 합쳐지면 \(\frac{(n+r-1)!}{(r-1)!n!} = \binom{n+r-1}{n}\)이 된다. 수렴구간은 \(|y| <1\)이다. 

PMF (Probability Mass Function) 확률 질량 함수 

확률 질량 함수란, 이산 확률 변수 X에 확률을 할당해주는 함수를 의미한다. $f(x) = P(X = x)$

어떤 함수 f 가 확률변수 X의 pmf가 되기 위해선 다음 세조건을 만족시켜야한다. (앞 두조건은 pmf의 기본 정의, 세번째는 X의  pmf이기 위한 조건)

1. \(f(x) \geq 0\)

2.\(\sum f(x) = 1\)

3.\(P(X \in  A) = \sum_{x \in A} f(x) \) : 직관적으로 잘 이해가 안되는 문장... 질문하기 

Support (set)

pmf f(x)가 항상 0보다 크거나 같게하는 x의 집합을 Support of X라고 한다. pmf의 도메인과 같은 개념 

Cumulative Distribution Function

$$F(x) = P(X \leq x)$$

구간별로 누적되는 함수이므로, pmf가 점차 쌓여가는 함수이다. Step function with jumps of size f(x) for \(x \in S(x)\)

 Expectations and Momentums 기댓값과 모멘텀

Expectation (=Mean)

기댓값 (expectation  value) 와 평균(Mean)은 같은 의미로, 표기법만 다르다. Expectation 은 E(x)로 표기하고, Mean은 \(\mu\)로 표기한다. 

$$ E(x) = \mu  = \sum x f(x)$$

Expectation 은 비단 x에 대해서만 구할 수 있는 것이 아니고, 일반적인 함수 g(x)에 대해서도 계산할 수 있다. 예를 들어 물리학에서 위치의 기댓값 뿐만아니라, 운동량이나 헤밀토니안등의 물리량의 Expectation value를 계산하는 경우를 아주 자주 볼 수 있다.

Expectation of g(X)  $$E[g(X)] = \sum g(x)f(x)$$

기댓값이 만족시키는 성질 

1. E(c)  = c 상수의 평균은 상수

2. E[ c g(X) ]  = c E[g(X)] 상수 곱은 그대로 적용

3.선형성 : \(E[c_1 g_1(X) + c_2g_2(X)] = c_1E[g_1(X)] + c_2E[g_2(X)]\)  이고, 이는 N개에 대해서도 당연히 성립한다. 

Moment

rth Moment of X :  \(\mu_{r}^{'} = E[X^r]$ : X의 r번째 모멘텀은 확률변수 X의 r제곱의 평균으로 정의한다. (이 제곱의 평균이 뒤에서 자주 쓰이기 때문에 정의해둔다.) 

rth central moment of X  : \(\mu_{r} = E[(X-\mu)^r]\) 

rth factorial moment of X : \(\mu_{r} = E[X(X-1)(X-2) ... (X-r +1)]$ : discrete에서 많이 쓴다. 

Variance 분산

$$Var(X) = E[(X-\mu)^2] = \sigma^2$$

로 정의한다. 이때 시그마는 Standard deviation 표준편차를 의미한다. \(\sigma = \sqrt{Var(X)}\) 또한

$$Var(x) = E[X^2] - \mu^2$$ 으로 정의한다. 

Proof : $$E[(X-\mu)^2] = E[X^2 - 2\mu X + \mu^2] = E[X^2] - 2 E(X)\mu + \mu^2 = E[X^2] - \mu^2$$

또 다음이 성립한다. 
E(aX+b) =\(aE(X)+b\)

Var(aX+b) = \(a^2 Var(X)\)

\(\sigma (aX+b) = a \sigma\)

 Moment generating function (MGF)

M(t) 로 보통 적는다. M(t) = $E(e^{tX})$ 이고, 0을 포함하는 구간 \(-h<t<h$에서 정의된다. 

우리는 0 근방에서 M(t)가 t에 대해 무한정으로 미분이 가능함을 알 수 있다. M(t)를 r번 t에 대해 미분하면 그 값은 \(E(X^r e^{tX})\) 일 것이다. 여기서 t에 0을 대입하면, 값은 $E(X^r)$이 된다. 바로 위에서 봤던 rth moment of X 이다.

  $$M^r(0) = E[X^r e^{tX}]_{t=0} = E[X^r] = \mu_{r}^{'}$$

이래서 mgf라는 이름이 붙었구나싶다. 

또한 M(t)의 정의에 따라 $$M(t) = E[e^{tX}] = \sum_{k=1}^{\infty}e^{tx_k}f(x_k) =\sum_{k=1}^{\infty}{p_k} e^{tX}$$

이고, 우리는 mgf로부터 역으로 pmf를 구할 수 있다. (대박)

예를 들어 mgf 가 아래와 같은 함수가 있다고 하자. 

$$M(t) = \frac{e^t}{2-e^t}$$ where $t<ln2$

모든 mgf 가 pmf와 exp항의 곱으로 전개될 수 있는 것은 아니지만, 이 mgf는 아래와 같이 geometric series로 전개가 가능하다. 

\(\frac{e^t}{2}$에 대해 매클로린 급수 전개를 진행하면 

$$\frac{\frac{e^t}{2}}{1-\frac{e^t}{2}} = \frac{e^t}{2}(1+\frac{e^t}{2} + (\frac{e^t}{2})^2+(\frac{e^t}{2})^3+ ...)$$

이를 다음과 같이 정리할 수 있다. 

$$= \frac{1}{2}e^t +(\frac{1}{2})^2e^{2t} + ... = \sum_{k=1}^{\infty} (\frac{1}{2})^k e^{tk}$$ 

따라서 우리가 찾는 pmf는 

$$\sum_{k=1}^{\infty} p_k e^{tk}= \sum_{k=1}^{\infty} (\frac{1}{2})^k e^{tk}$$

$$f(x) = (\frac{1}{2})^k$$

 

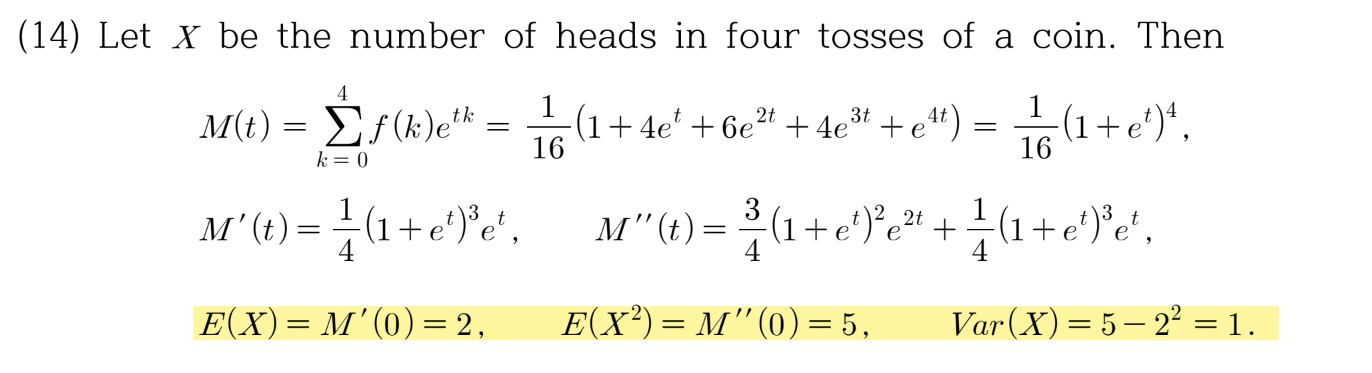
위에 예시에서, 확률변수 X는 동전을 4번 던졌을때 나오는 앞면의 횟수이므로,  f(k)는 앞면이  k 번 나올때의 확률을 의미한다. M(t)를 구해주면 \(e^{tX}\) 의 평균을 구해주면 되는 것이고, 그렇게 얻은 mgf는 우리가 E(X)가 필요할때는 한번 미분해서 t=0 넣고, Var(X)가 필요할 때는 두번미분해서 얻은 모멘트와 평균의 제곱을 빼서 구한다.